■ブログの趣旨はこちらの記事を確認のこと。 http://english123.blog.shinobi.jp/%E9%9B%91%E8%A8%98/%E3%83%96%E3%83%AD%E3%82%B0%E3%81%AB%E3%81%A4%E3%81%84%E3%81%A6
ある社会人の勉強記録
カテゴリー「物理化学」の記事一覧
- 2025.01.31 [PR]
- 2013.11.18 次世代電池に必要なこと。
- 2013.11.02 クラウジウスの不等式の証明とエントロピーの定義
- 2013.10.06 カルノーの定理の証明とクラウジウスの不等式導入
- 2013.10.05 カルノーサイクル入門:理想気体のカルノー効率について
- 2013.10.05 熱力学の大ニ法則:トムソンの原理「ケルビンの原理」とクラウジウスの原理、オストワルドの原理
[PR]
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
次世代電池に必要なこと。
色々な化学ニュースで容量のいい電池が新聞に載り、
凄い研究であるかの様に発表されるが、僕から提言したいことが一つある。
もう少し、色々な視点でそのニュース記事を報告してほしい。
何故なら、「電池に必要な特性は、容量だけではない」からだ。
専門的なことでいうと、下記のような点はピックアップしてほしい。
=========================================================---====
①安全性
(⇒エネルギーが高い材料になっているのに安全なのかという視点をもってほしい。エネルギーの高い材料はいくらでもあるが、安全か??という視点が加わるだけで途端に技術的なハードルがあがるからだ)
②自己放電特性
(⇒自己放電とは、勝手に容量が減少する現象。外部回路と接続していないのに、放電容量が保存環境によって減少することは多々ある。いくら優れた材料でも、自己放電が頻発するような電池なら材料としてのメリットは希薄。この辺の解決は技術的に難しいからこそ、次世代電池ではここを論じるべきだ。論じないのであれば、問題の先送りに過ぎないのでは?)
③サイクル特性
(⇒二次電池のニュースとかで、容量だけ論じてサイクルには全く言及しないことがあるが、サイクル特性は二次電池の最もベーシックな特性だと思われる。容量があっても寿命が短ければしょうがないわけだし、容量を論じるなら最低でもサイクルを論じないと電池のニュースとして意味がない気がする。二次電池になるのかならないのか。二次電池でなくても、一次電池ならビジネスになるのかなどが重要な視点です。)
④温度特性
電池を使う温度は色々ありうる。どういった温度で使えるのか?という視点は商品を作る上で極めて重要。使える温度でデバイスが限定されてしまうと言っても過言ではなく、低温で使えないなら一部地域では使えないことになり、モバイル端末に向くのか疑問。
=========================================================---====
これと⑤容量を論じてほしい。こういった視点が加わるだけで技術的な実現可能性がわかりやすくなる。
当然、電池の課題はこれだけではないのだが、「電池の課題抽出をしましょう。」というときに
最低でもこういった視点がニュースに乗らなければ意味がないと思うのです。何故なら、この辺が技術的に電池の商品化に必要かつ難しい技術開発だからです。
大学の研究機関もこういったことを意識して次世代電池を作ってほしい。
凄い研究であるかの様に発表されるが、僕から提言したいことが一つある。
もう少し、色々な視点でそのニュース記事を報告してほしい。
何故なら、「電池に必要な特性は、容量だけではない」からだ。
専門的なことでいうと、下記のような点はピックアップしてほしい。
=========================================================---====
①安全性
(⇒エネルギーが高い材料になっているのに安全なのかという視点をもってほしい。エネルギーの高い材料はいくらでもあるが、安全か??という視点が加わるだけで途端に技術的なハードルがあがるからだ)
②自己放電特性
(⇒自己放電とは、勝手に容量が減少する現象。外部回路と接続していないのに、放電容量が保存環境によって減少することは多々ある。いくら優れた材料でも、自己放電が頻発するような電池なら材料としてのメリットは希薄。この辺の解決は技術的に難しいからこそ、次世代電池ではここを論じるべきだ。論じないのであれば、問題の先送りに過ぎないのでは?)
③サイクル特性
(⇒二次電池のニュースとかで、容量だけ論じてサイクルには全く言及しないことがあるが、サイクル特性は二次電池の最もベーシックな特性だと思われる。容量があっても寿命が短ければしょうがないわけだし、容量を論じるなら最低でもサイクルを論じないと電池のニュースとして意味がない気がする。二次電池になるのかならないのか。二次電池でなくても、一次電池ならビジネスになるのかなどが重要な視点です。)
④温度特性
電池を使う温度は色々ありうる。どういった温度で使えるのか?という視点は商品を作る上で極めて重要。使える温度でデバイスが限定されてしまうと言っても過言ではなく、低温で使えないなら一部地域では使えないことになり、モバイル端末に向くのか疑問。
=========================================================---====
これと⑤容量を論じてほしい。こういった視点が加わるだけで技術的な実現可能性がわかりやすくなる。
当然、電池の課題はこれだけではないのだが、「電池の課題抽出をしましょう。」というときに
最低でもこういった視点がニュースに乗らなければ意味がないと思うのです。何故なら、この辺が技術的に電池の商品化に必要かつ難しい技術開発だからです。
大学の研究機関もこういったことを意識して次世代電池を作ってほしい。
PR
クラウジウスの不等式の証明とエントロピーの定義
久しぶりに、熱力学の記事を書きます。前回の記事を思い出せば、高温熱源と低温熱源の二つを組み合わせたサイクルについて論じてきたけれども、熱源の個数にしばられずもう少し一般的な関係を調べたのがクラウジウスの不等式です。このクラウジウスの不等式の証明ですが、初学者から見ると全くもって意味不明だと思う。私も学生時代意味不明でした。なので、力が及ばないかもしれないが丁寧に解説していこうと思う。そこで次の図を見てほしい。
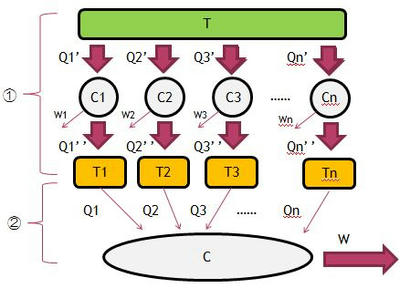
まず①の部分について、これは温度Tの熱源を利用して、
可逆サイクルC1,C2,C3~Cnを動かす図です。よくわからなければC1を見てみよう。
C1の場合、温度Tの熱源があって、その熱源から熱Q1'を受け取ってサイクルC1を動かしています。
C1は仕事W1をするとともに熱を供給します。この熱をQ1’’とし、
Q1の熱を温度T1の熱源に熱を運んでいるのです。
これをn個のサイクルで行い、それぞれ温度T1からTnの熱源に熱を運んでいます。
この場合、前回の記事を思い出せば、
任意のサイクルCkに対して、下記の式が成り立ちます。
Qk'/T + Qk''/Tk =0 ……A
また、n個のサイクル(k=1~n)で上の等式を足し合わせると、下記の式が成り立ちます。
(1/T)*ΣQk' + Σ(Qk”/Tk)=0 …B
ここまでが①の部分でやっている操作であり、この複数の熱機関について
A式、B式が成り立つのは自明です。
次に②の部分を説明します。先ほど登場したn個の熱源から熱Q1~QnをサイクルCにおくって
仕事Wをさせる図です。一見すると、この図はトムソンの原理に反していそうですが、
Q1からQnの中に負の熱があってもいいのです。
負の熱があってもいいということを聞くとこれも何だかよくわからなくなりますが、
熱源を少なくするとイメージしやすいです。そこで下の図をみてください。

この図の②-①だと、熱源はT1,T2,T3しかありません。このうち、T1,T2が正の熱Q1,Q2を放出し、
T3がQ3の熱を受け取るものだと考えます。
これって、普通のサイクルと同じことをやっているのに気がつきませんか?
だって②-①のようにT1,T2が正の熱Q1,Q2を放出し、T3がQ3の熱を受け取るということは
②-②のように普通のサイクルに書き換えられるじゃないですか。
②-①と②-②のはやっていることが完全に同じなのです。熱を送る側の熱源だけ書いて
負でもよいというとどうもイメージがわかないのですが、これと同じだと理解すると
この記述の意味が想像できると思います。何個かの熱源が負で何個かの熱源が正という前提だから
よく関係が整理できないのだけれども、少数の熱源に絞って考えれば意味がわかるんじゃないかと
勝手に思っていますが、それでも意味がわからなかったらすみません。
このようにして、熱源T1,T2,~Tnと②のサイクルは連結できるのです。
さて②での熱のやり取りQ1を-Q1”と等しくなるように操作するとします。
すると、B式から下記の関係が成り立ちます。
(1/T)*ΣQk' = Σ(Qk/Tk) …C
いい関係式が得られましたね。ここで考えたいのですが、ΣQkは正でしょうか負でしょうか。
実は、ΣQk>0だとするとトムソンの原理に反してしまうのです。
従ってΣQk≦0(サイクル②が可逆サイクルなら=)となります。
すなわち、下記の関係式を得ます。
ΣQk/Tk ≦ 0…D
更に、n⇒∞に近づけていくと下記の式を得ます。
∮d’Q/T≦ 0…D'
このD'式がクラウジウスの不等式です。準静的過程の場合、
∮d’Q/T=0であり、d’Q/Tは状態量として扱えることが確認できます。
この新しい状態量はエントロピーと呼ばれるものです。エントロピーをSとすると、
下記の式で定義できます。
S = d'Q/T…E
次回はこのエントロピーの性質について論じたいと思います。
まず①の部分について、これは温度Tの熱源を利用して、
可逆サイクルC1,C2,C3~Cnを動かす図です。よくわからなければC1を見てみよう。
C1の場合、温度Tの熱源があって、その熱源から熱Q1'を受け取ってサイクルC1を動かしています。
C1は仕事W1をするとともに熱を供給します。この熱をQ1’’とし、
Q1の熱を温度T1の熱源に熱を運んでいるのです。
これをn個のサイクルで行い、それぞれ温度T1からTnの熱源に熱を運んでいます。
この場合、前回の記事を思い出せば、
任意のサイクルCkに対して、下記の式が成り立ちます。
Qk'/T + Qk''/Tk =0 ……A
また、n個のサイクル(k=1~n)で上の等式を足し合わせると、下記の式が成り立ちます。
(1/T)*ΣQk' + Σ(Qk”/Tk)=0 …B
ここまでが①の部分でやっている操作であり、この複数の熱機関について
A式、B式が成り立つのは自明です。
次に②の部分を説明します。先ほど登場したn個の熱源から熱Q1~QnをサイクルCにおくって
仕事Wをさせる図です。一見すると、この図はトムソンの原理に反していそうですが、
Q1からQnの中に負の熱があってもいいのです。
負の熱があってもいいということを聞くとこれも何だかよくわからなくなりますが、
熱源を少なくするとイメージしやすいです。そこで下の図をみてください。
この図の②-①だと、熱源はT1,T2,T3しかありません。このうち、T1,T2が正の熱Q1,Q2を放出し、
T3がQ3の熱を受け取るものだと考えます。
これって、普通のサイクルと同じことをやっているのに気がつきませんか?
だって②-①のようにT1,T2が正の熱Q1,Q2を放出し、T3がQ3の熱を受け取るということは
②-②のように普通のサイクルに書き換えられるじゃないですか。
②-①と②-②のはやっていることが完全に同じなのです。熱を送る側の熱源だけ書いて
負でもよいというとどうもイメージがわかないのですが、これと同じだと理解すると
この記述の意味が想像できると思います。何個かの熱源が負で何個かの熱源が正という前提だから
よく関係が整理できないのだけれども、少数の熱源に絞って考えれば意味がわかるんじゃないかと
勝手に思っていますが、それでも意味がわからなかったらすみません。
このようにして、熱源T1,T2,~Tnと②のサイクルは連結できるのです。
さて②での熱のやり取りQ1を-Q1”と等しくなるように操作するとします。
すると、B式から下記の関係が成り立ちます。
(1/T)*ΣQk' = Σ(Qk/Tk) …C
いい関係式が得られましたね。ここで考えたいのですが、ΣQkは正でしょうか負でしょうか。
実は、ΣQk>0だとするとトムソンの原理に反してしまうのです。
従ってΣQk≦0(サイクル②が可逆サイクルなら=)となります。
すなわち、下記の関係式を得ます。
ΣQk/Tk ≦ 0…D
更に、n⇒∞に近づけていくと下記の式を得ます。
∮d’Q/T≦ 0…D'
このD'式がクラウジウスの不等式です。準静的過程の場合、
∮d’Q/T=0であり、d’Q/Tは状態量として扱えることが確認できます。
この新しい状態量はエントロピーと呼ばれるものです。エントロピーをSとすると、
下記の式で定義できます。
S = d'Q/T…E
次回はこのエントロピーの性質について論じたいと思います。
カルノーの定理の証明とクラウジウスの不等式導入
■カルノーの定理の証明
前回、カルノーサイクルの概要と効率の計算の仕方を論じました。
今回はもう少し議論を発展させて、カルノーの定理について論じます。カルノーの定理の前に一つ論じておくことがあります。それは、カルノーサイクルが可逆か不可逆かです。カルノーサイクルは、結論からいうと可逆機関です。そもそも、カルノーサイクル自体が可逆過程を組み合わせたものであり、逆に回すことも可能なのです。そこを踏まえたうえでカルノーの定理を考えてみましょう。カルノーの定理とは、下記の定理です。
■定まった高温熱源と低温熱源の間に働く熱機関サイクルのうち、全ての可逆サイクルは等しく最大であり、不可逆サイクルは必ずそれより小さい。
何の話をしているかというと、こういうことです。「高温熱源と低温熱源がある熱機関だとカルノーサイクル(可逆サイクル)は全部同じ効率であり、カルノーサイクルが最大効率を持ったサイクルです。よって、不可逆サイクルはそれより効率が低くなります」といっているのです。
よく、オットーサイクルやランキンサイクル等の実サイクルも可逆サイクルだから、カルノーの定理よりカルノーサイクルと同じ効率では?と思われる方がいる。そもそも前提である熱源の個数がずれています。カルノーの定理は【ただ2つの熱源の間で動作する可逆機関】を対象として議論をしています。でも、実サイクルはそうではありません。例えば、実サイクルの可逆機関では等圧変化過程や等積変化過程があります。これらの過程では必ず熱の出入りがあります。準静的変化(可逆変化)では,熱の移動の時に温度差があってはいけませんから例えば等圧変化で温度が Ta から Tb まで変化したとすると,熱をやりとりする相手の熱源は温度が Ta から Tb までの連続無限個のものが必要になります.
したがって,カルノーサイクル以外のものは【ただ2つの熱源の間で動作する可逆機関】ではないのです。ここは誤解しないでください。同じディスカッションがYahoo知恵袋にありますので紹介しておきます。
http://okwave.jp/qa/q5374013.html
じゃあ、何故カルノーの定理が成り立つのか。今回はこれについて解説しようと思います。
すべての可逆サイクル(カルノーサイクル)の効率は等しい。
(証明)可逆サイクルAと可逆サイクルBの効率をηAとηBを定義する。今、ηA>ηBだと仮定しサイクルAとサイクルBを連結したサイクルを考える。(下図参考)
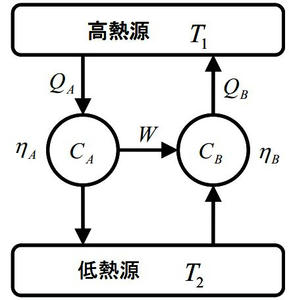
上のサイクルではηA>ηBより、W/QA > W/QB ⇔QB > QAとなるが、この場合低温熱源から高温熱源に移動することになり、熱力学の第二法則に反する。よってηA≦Bでなければならない。
※そもそも可逆サイクル同士の組み合わせですから、このケースの場合、何の影響も残さずに低温熱源から高温熱源に熱を移動させていますよね。
じゃあ、ηA<ηBとなる場合はどうかというと、下記の図を見てください。
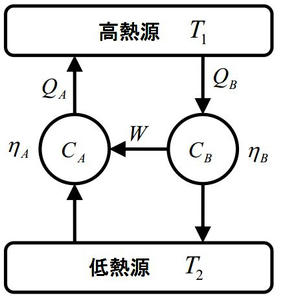
図のように可逆サイクルを回すとηA<ηB⇔W/QA<W/QB⇔QB<QAとなり、低温熱源から高温熱源に何の影響も残さず可逆的に熱の移動ができてしまう。これもまた矛盾だといえます。
二つの熱源の場合、可逆機関の熱効率はηA=ηBとなり等しくならざるをえないのです。
不可逆サイクルの効率は必ず可逆サイクル(カルノーサイクル)に劣る。
これを証明するために、可逆サイクルと不可逆サイクルを組み合わせた図のようなサイクルを考えましょう。

不可逆サイクルの効率をη’、可逆サイクルの効率をηとする。
η’>ηと仮定すると、W/Q'>W/Q⇔Q>Q'となり、やはり熱力学第二法則に矛盾する。よってη’≦ηとなる。更にη’=ηとするとQ'=Qとなるが、これでは不可逆サイクルと可逆サイクルの連結サイクルが可逆サイクルになってしまうので矛盾しています。以上より、η’<ηとならざるをえないのです。
これにより二つの熱源からなる可逆サイクル(カルノーサイクル)こそが、最大の熱効率を誇る熱機関だということが証明されました。更に、カルノー効率は前回の記事によると
η = 1- TL/TH = (TH - TL)/TH < 1です。
従って、η=1となる熱機関は作ることができないのです。第二種永久機関は存在しない。カルノーの功績から定量的に理解できると思います。それにもかかわらず、カルノー自身は熱力学第二法則の発見者ではないのですよね。それでも、物理学が進んだ現代だからカルノーの功績の素晴らしさは理解できるものだと思いますよ。
追記:実はこれまで理想気体でカルノー効率を定義したので、腑に落ちないかもしれませんがやはり実在気体であっても上のような効率になります。やはりすべてのカルノーサイクルは同等なのです。これを導出するヒントは、http://qanda.rakuten.ne.jp/qa1885802.htmlに論じられていますが、暇な時やっておきます。
■クラウジウスの不等式
さて、ここまで二つの熱源に対して下記が成り立つことを論じました。
QH/TH + QL/TL = 0 …①
不可逆過程の場合は、上の=が成り立ちません。カルノーの定理より
η = W/QH = (QH+QL)/QH < (TH - TL)/TH
⇔1 + QL/QH < 1 - TL/TH
⇔QL/QH + TL/TH < 0
⇔QL/TL + TH/QH <0…②
となります。従って一般の機関に対して下記が成り立つのは自明です。
QH/TH + QL/TL ≦ 0 …③
さて、2個の熱源で上の式が成り立つことがわかりました。
これをN個の熱源に拡張した議論がクラウジウスの不等式です。
クラウジウスの不等式では複数個の熱源に対して下記が成り立つという議論です。
ΣQi/Ti ≦0(∞個の熱源に拡張すると∮dQ/T≦0)
では、何故この式が成り立つのか?次回の記事ではそれについて論じようと思います。
前回、カルノーサイクルの概要と効率の計算の仕方を論じました。
今回はもう少し議論を発展させて、カルノーの定理について論じます。カルノーの定理の前に一つ論じておくことがあります。それは、カルノーサイクルが可逆か不可逆かです。カルノーサイクルは、結論からいうと可逆機関です。そもそも、カルノーサイクル自体が可逆過程を組み合わせたものであり、逆に回すことも可能なのです。そこを踏まえたうえでカルノーの定理を考えてみましょう。カルノーの定理とは、下記の定理です。
■定まった高温熱源と低温熱源の間に働く熱機関サイクルのうち、全ての可逆サイクルは等しく最大であり、不可逆サイクルは必ずそれより小さい。
何の話をしているかというと、こういうことです。「高温熱源と低温熱源がある熱機関だとカルノーサイクル(可逆サイクル)は全部同じ効率であり、カルノーサイクルが最大効率を持ったサイクルです。よって、不可逆サイクルはそれより効率が低くなります」といっているのです。
よく、オットーサイクルやランキンサイクル等の実サイクルも可逆サイクルだから、カルノーの定理よりカルノーサイクルと同じ効率では?と思われる方がいる。そもそも前提である熱源の個数がずれています。カルノーの定理は【ただ2つの熱源の間で動作する可逆機関】を対象として議論をしています。でも、実サイクルはそうではありません。例えば、実サイクルの可逆機関では等圧変化過程や等積変化過程があります。これらの過程では必ず熱の出入りがあります。準静的変化(可逆変化)では,熱の移動の時に温度差があってはいけませんから例えば等圧変化で温度が Ta から Tb まで変化したとすると,熱をやりとりする相手の熱源は温度が Ta から Tb までの連続無限個のものが必要になります.
したがって,カルノーサイクル以外のものは【ただ2つの熱源の間で動作する可逆機関】ではないのです。ここは誤解しないでください。同じディスカッションがYahoo知恵袋にありますので紹介しておきます。
http://okwave.jp/qa/q5374013.html
じゃあ、何故カルノーの定理が成り立つのか。今回はこれについて解説しようと思います。
すべての可逆サイクル(カルノーサイクル)の効率は等しい。
(証明)可逆サイクルAと可逆サイクルBの効率をηAとηBを定義する。今、ηA>ηBだと仮定しサイクルAとサイクルBを連結したサイクルを考える。(下図参考)
上のサイクルではηA>ηBより、W/QA > W/QB ⇔QB > QAとなるが、この場合低温熱源から高温熱源に移動することになり、熱力学の第二法則に反する。よってηA≦Bでなければならない。
※そもそも可逆サイクル同士の組み合わせですから、このケースの場合、何の影響も残さずに低温熱源から高温熱源に熱を移動させていますよね。
じゃあ、ηA<ηBとなる場合はどうかというと、下記の図を見てください。
図のように可逆サイクルを回すとηA<ηB⇔W/QA<W/QB⇔QB<QAとなり、低温熱源から高温熱源に何の影響も残さず可逆的に熱の移動ができてしまう。これもまた矛盾だといえます。
二つの熱源の場合、可逆機関の熱効率はηA=ηBとなり等しくならざるをえないのです。
不可逆サイクルの効率は必ず可逆サイクル(カルノーサイクル)に劣る。
これを証明するために、可逆サイクルと不可逆サイクルを組み合わせた図のようなサイクルを考えましょう。
不可逆サイクルの効率をη’、可逆サイクルの効率をηとする。
η’>ηと仮定すると、W/Q'>W/Q⇔Q>Q'となり、やはり熱力学第二法則に矛盾する。よってη’≦ηとなる。更にη’=ηとするとQ'=Qとなるが、これでは不可逆サイクルと可逆サイクルの連結サイクルが可逆サイクルになってしまうので矛盾しています。以上より、η’<ηとならざるをえないのです。
これにより二つの熱源からなる可逆サイクル(カルノーサイクル)こそが、最大の熱効率を誇る熱機関だということが証明されました。更に、カルノー効率は前回の記事によると
η = 1- TL/TH = (TH - TL)/TH < 1です。
従って、η=1となる熱機関は作ることができないのです。第二種永久機関は存在しない。カルノーの功績から定量的に理解できると思います。それにもかかわらず、カルノー自身は熱力学第二法則の発見者ではないのですよね。それでも、物理学が進んだ現代だからカルノーの功績の素晴らしさは理解できるものだと思いますよ。
追記:実はこれまで理想気体でカルノー効率を定義したので、腑に落ちないかもしれませんがやはり実在気体であっても上のような効率になります。やはりすべてのカルノーサイクルは同等なのです。これを導出するヒントは、http://qanda.rakuten.ne.jp/qa1885802.htmlに論じられていますが、暇な時やっておきます。
■クラウジウスの不等式
さて、ここまで二つの熱源に対して下記が成り立つことを論じました。
QH/TH + QL/TL = 0 …①
不可逆過程の場合は、上の=が成り立ちません。カルノーの定理より
η = W/QH = (QH+QL)/QH < (TH - TL)/TH
⇔1 + QL/QH < 1 - TL/TH
⇔QL/QH + TL/TH < 0
⇔QL/TL + TH/QH <0…②
となります。従って一般の機関に対して下記が成り立つのは自明です。
QH/TH + QL/TL ≦ 0 …③
さて、2個の熱源で上の式が成り立つことがわかりました。
これをN個の熱源に拡張した議論がクラウジウスの不等式です。
クラウジウスの不等式では複数個の熱源に対して下記が成り立つという議論です。
ΣQi/Ti ≦0(∞個の熱源に拡張すると∮dQ/T≦0)
では、何故この式が成り立つのか?次回の記事ではそれについて論じようと思います。
カルノーサイクル入門:理想気体のカルノー効率について
カルノーサイクルの熱力学的な意味はさておき、まずはどんなサイクルなのか紹介しようと思います。下記画像をご覧ください。

状態A,B,C,DをそれぞれA(Pa,Va,Ta),B(Pb,Vb,Tb),C(Pc,Vc,Tc),D(Pd,Vd,Td)とします。
カルノーサイクルの場合、下記のような4つの可逆変化を行うサイクルとなっています。
A⇒B:等温膨張
B⇒C:断熱膨張
C⇒D:等温圧縮
D⇒A:断熱圧縮
入力した熱量Qin、外部にしたトータルの仕事Wtを用いて熱機関の効率ηは一般的にη= Wt/Qinとなります。本日の議題は理想気体でカルノーサイクルにおける効率ηを計算してみようということです。(カルノーサイクルにおける効率をカルノー効率といいます。)小難しいことは考えず一個一個のプロセスで熱力学の第一法則を立ててみましょう。
■A⇒B:等温膨張
ΔUab = Qab + Wab …①
等温なので、Ta = Tb。また理想気体だとΔUab=0となる。よって
Qab= -Wab = ∫PdV = nRTa*dV/V = nRTa*Ln(Vb/Va)…②
■B⇒C:断熱膨張
ΔUbc = Qbc + Wbc …③
断熱過程なのでQbc = 0となる。従って、
Wbc = U(Tc) - U(Tb) = U(Tc) - U(Ta) … ④
■C⇒D:等温圧縮
ΔUcd = Qcd + Wcd …⑤
等温なので、Tc = Td。また理想気体だとΔUcd=0となる。よって
Qcd= -Wcd = ∫PdV = nRTc*dV/V = nRTc*Ln(Vd/Vc)…⑥
■D⇒A:断熱圧縮
ΔUda = Qda + Wda …⑦
断熱過程なのでQbc = 0となる。従って、
Wda = U(Ta) - U(Td) = U(Ta) - U(Tc) … ⑧
以上より、正味の仕事Wtは④、⑧を代入すると次式のようになる。
Wt = -(Wab + Wbc + Wcd + Wda) = -(Wab + Wcd) = Qab + Qcd
よって、熱効率ηはQin = Qabとなるので次式の通りになる。
η = (Qab + Qcd)/Qab = 1 + Qcd/Qab…⑨
大分本質的な形になりましたね。
QcdとQabに②式と⑥式を代入しましょう。すると、
η = 1 + (Tc/Ta)*Ln(Vb/Va)/{Ln(Vd/Vc)}…⑩
ここで、ポアソンの関係式を思い出すと下記が成り立ちます。
Vb^(γ‐1)*Tb = Vb^(γ‐1)*Ta = Vc^(γ‐1)*Tc…⑪
Vd^(γ‐1)*Td = Vd^(γ‐1)*Tc = Va^(γ‐1)*Ta…⑫
⑪×⑫⇔(Vb*Vd)^(γ‐1) = (Va*Vc)^(γ‐1) …⑬
∴Vb*Vd= Va*Vc ⇔ Vb/Va = Vc/Vd…⑬'
⑬’を⑩に代入すると、下記のようになります。
η = 1 + Qcd/Qab =1 - (Tc/Ta) …⑭
ここで、おさらい。Qabは高温熱源からの熱源を表していますのでQH,Qcdは低温熱源からの熱を表していますのでQLと書くことにします。またTa、Tcも同様にTH,TLと表記します。世の一般的な教科書では、下記のように書くほうが一般的かもしれません。
η = 1 + QL/QH =1 - (TL/TH) …⑭’
更に、⑭式を見てわかるようにカルノーサイクルでは下記の式が成り立ちます。
QL/QH = -(TL/TH)
QL/TL + QH/TL = 0…⑮
この⑮式こそ、エントロピーの発見につながる重要な式なのです。この話はのちにクラウジウスの不等式の話でします。カルノーサイクルとカルノー効率はここまでです。
状態A,B,C,DをそれぞれA(Pa,Va,Ta),B(Pb,Vb,Tb),C(Pc,Vc,Tc),D(Pd,Vd,Td)とします。
カルノーサイクルの場合、下記のような4つの可逆変化を行うサイクルとなっています。
A⇒B:等温膨張
B⇒C:断熱膨張
C⇒D:等温圧縮
D⇒A:断熱圧縮
入力した熱量Qin、外部にしたトータルの仕事Wtを用いて熱機関の効率ηは一般的にη= Wt/Qinとなります。本日の議題は理想気体でカルノーサイクルにおける効率ηを計算してみようということです。(カルノーサイクルにおける効率をカルノー効率といいます。)小難しいことは考えず一個一個のプロセスで熱力学の第一法則を立ててみましょう。
■A⇒B:等温膨張
ΔUab = Qab + Wab …①
等温なので、Ta = Tb。また理想気体だとΔUab=0となる。よって
Qab= -Wab = ∫PdV = nRTa*dV/V = nRTa*Ln(Vb/Va)…②
■B⇒C:断熱膨張
ΔUbc = Qbc + Wbc …③
断熱過程なのでQbc = 0となる。従って、
Wbc = U(Tc) - U(Tb) = U(Tc) - U(Ta) … ④
■C⇒D:等温圧縮
ΔUcd = Qcd + Wcd …⑤
等温なので、Tc = Td。また理想気体だとΔUcd=0となる。よって
Qcd= -Wcd = ∫PdV = nRTc*dV/V = nRTc*Ln(Vd/Vc)…⑥
■D⇒A:断熱圧縮
ΔUda = Qda + Wda …⑦
断熱過程なのでQbc = 0となる。従って、
Wda = U(Ta) - U(Td) = U(Ta) - U(Tc) … ⑧
以上より、正味の仕事Wtは④、⑧を代入すると次式のようになる。
Wt = -(Wab + Wbc + Wcd + Wda) = -(Wab + Wcd) = Qab + Qcd
よって、熱効率ηはQin = Qabとなるので次式の通りになる。
η = (Qab + Qcd)/Qab = 1 + Qcd/Qab…⑨
大分本質的な形になりましたね。
QcdとQabに②式と⑥式を代入しましょう。すると、
η = 1 + (Tc/Ta)*Ln(Vb/Va)/{Ln(Vd/Vc)}…⑩
ここで、ポアソンの関係式を思い出すと下記が成り立ちます。
Vb^(γ‐1)*Tb = Vb^(γ‐1)*Ta = Vc^(γ‐1)*Tc…⑪
Vd^(γ‐1)*Td = Vd^(γ‐1)*Tc = Va^(γ‐1)*Ta…⑫
⑪×⑫⇔(Vb*Vd)^(γ‐1) = (Va*Vc)^(γ‐1) …⑬
∴Vb*Vd= Va*Vc ⇔ Vb/Va = Vc/Vd…⑬'
⑬’を⑩に代入すると、下記のようになります。
η = 1 + Qcd/Qab =1 - (Tc/Ta) …⑭
ここで、おさらい。Qabは高温熱源からの熱源を表していますのでQH,Qcdは低温熱源からの熱を表していますのでQLと書くことにします。またTa、Tcも同様にTH,TLと表記します。世の一般的な教科書では、下記のように書くほうが一般的かもしれません。
η = 1 + QL/QH =1 - (TL/TH) …⑭’
更に、⑭式を見てわかるようにカルノーサイクルでは下記の式が成り立ちます。
QL/QH = -(TL/TH)
QL/TL + QH/TL = 0…⑮
この⑮式こそ、エントロピーの発見につながる重要な式なのです。この話はのちにクラウジウスの不等式の話でします。カルノーサイクルとカルノー効率はここまでです。
熱力学の大ニ法則:トムソンの原理「ケルビンの原理」とクラウジウスの原理、オストワルドの原理
皆様も経験的にしっていることでしょうが、温めたコーヒーが時間とともに冷えていくことはありますよね。では、その逆の現象が起こると思いますか。冷え切ったコーヒーが時間とともに温まっていくということです。皆様はやはり経験的にそれが起きないことをしっているでしょう。冷えたものが温まらない。この熱の不可逆的性質こそが熱力学の第二法則と呼ばれる基本原理です。これを学問的に厳密に表現した人がいます。それが、クラウジウス、トムソン、オストワルドらです。彼らは、こういった熱の不可逆性をどのように論じたのでしょうか?熱力学第二法則の導入として、今回はトムソンの原理とクラウジウスの原理、オストワルドの原理を解説します。
■トムソンの原理
物理学の教科書では次のように書いてあります。
一つの熱源から正の熱を受け取り、これを全て仕事に変える以外に他に何の痕跡も残さないようにすることは出来ない。
最初この意味がわかりませんでした。でも、この文中の以外を除くという意味ではなく、”だけではなくて”というニュアンスでとらえるとなんとなく意味がわかりました。具体的には下記の通りです。
「一つの熱源から正の熱を受け取り、これを全て仕事に変えるだけでなく、他に何の痕跡も残さないようにすること」は出来ない。
日本語って難しいですね。つまり、熱源から正の熱を受け取り、これを全て仕事に変えると何か痕跡が残るため、痕跡が残らないようにはできないという意味になります。
だったら最初から混乱しないように「 他に何も変化を残さずに、一定温度の熱源から熱を取り出して、それを全て仕事に変換することは不可能である。」 という主張を 『 トムソンの原理 』 であると記述してほしいです。
ここで新たな疑問が浮上します。痕跡を残せば熱源の熱はすべて仕事に変換できるのかということです。どうやら、熱を全て仕事にできないという単純な法則ではないからこういう日本語なのだろう。
例えば、気体の等温膨張を考えてみよう。この場合、熱力学の第一法則を考えると下記のようになる。
dU = d'q + d'w = 0
d'q = -d'w
どうやら等温膨張の場合は熱を全て仕事に変えられるではないか。しかし、この場合気体の内圧は減少し体積も膨張してしまう。どうやら、トムソンの原理で言及している議論は熱機関のサイクルを意識したものでしょう。内圧を減少させたり、体積膨張させずに熱を全て仕事に変えるのは無理ですよというのがトムソンの原理です。等温環境下で熱を加えたら膨張して仕事をするが、膨張しきったら膨張しておしまいなのです。状態を変えずに熱から仕事は取り出せません。これがトムソンの原理です。等温膨張と混同してはいけませんよ。
■クラウジウスの原理
物理学の教科書では次のように書いてあります。
低温の熱源から高温の熱源に正の熱を移す以外に、 他に何の痕跡も残さないようにすることは出来ない。
同じように解釈すると、他に何も変化を残さずに、低温物体から高温物体へ熱を移すことは不可能であるという意味になります。クラウジウスの原理は経験的にわかりやすいかもしれません。低温熱源と高温熱源を置いておくと何もしなくても(何の状態も変えなくても)高温熱源に低温熱源から熱が移動できてしてしまう。しかし、そんなことは起こり得ないことなど皆さんもご存じでしょう。
■クラウジウスの原理とトムソンの原理の同等性
クラウジウスの原理とトムソンの原理は、実は全く同じなのです。クラウジウスの原理がなりたてば、トムソンの原理がなりたつし、トムソンの原理が成り立てばクラウジウスの原理もなりたちます。子の証明については、下記のサイトの説明にゆだねます。確認のほどよろしくお願いします。
参考1)http://homepage3.nifty.com/rikei-index01/neturiki/neturiki2nado.html
参考2)http://camellia.thyme.jp/files/html/thermo20130322/node56.html
■オストワルドの原理
これは非常にシンプルな原理です。第2種永久機関は存在しない。第二種永久機関とは、「一つの熱源から正の熱を受け取り、これを全て仕事に変える以外に、 他に何の痕跡も残さないような機関」のことです。必然的にトムソンの原理が成り立てばオストワルドの原理もなりたつのです。第二種という表現から第一種はなんだという疑問が生じますよね。永久機関は昔の人のロマンでした。
第一種永久機関=無からエネルギーを生み出す熱機関
第二種永久機関=元の状態に戻りながら熱エネルギーを100%仕事にする熱機関
として、研究されてきたのですが第二種永久機関は存在しないのです。
■トムソンの原理
物理学の教科書では次のように書いてあります。
一つの熱源から正の熱を受け取り、これを全て仕事に変える以外に他に何の痕跡も残さないようにすることは出来ない。
最初この意味がわかりませんでした。でも、この文中の以外を除くという意味ではなく、”だけではなくて”というニュアンスでとらえるとなんとなく意味がわかりました。具体的には下記の通りです。
「一つの熱源から正の熱を受け取り、これを全て仕事に変えるだけでなく、他に何の痕跡も残さないようにすること」は出来ない。
日本語って難しいですね。つまり、熱源から正の熱を受け取り、これを全て仕事に変えると何か痕跡が残るため、痕跡が残らないようにはできないという意味になります。
だったら最初から混乱しないように「 他に何も変化を残さずに、一定温度の熱源から熱を取り出して、それを全て仕事に変換することは不可能である。」 という主張を 『 トムソンの原理 』 であると記述してほしいです。
ここで新たな疑問が浮上します。痕跡を残せば熱源の熱はすべて仕事に変換できるのかということです。どうやら、熱を全て仕事にできないという単純な法則ではないからこういう日本語なのだろう。
例えば、気体の等温膨張を考えてみよう。この場合、熱力学の第一法則を考えると下記のようになる。
dU = d'q + d'w = 0
d'q = -d'w
どうやら等温膨張の場合は熱を全て仕事に変えられるではないか。しかし、この場合気体の内圧は減少し体積も膨張してしまう。どうやら、トムソンの原理で言及している議論は熱機関のサイクルを意識したものでしょう。内圧を減少させたり、体積膨張させずに熱を全て仕事に変えるのは無理ですよというのがトムソンの原理です。等温環境下で熱を加えたら膨張して仕事をするが、膨張しきったら膨張しておしまいなのです。状態を変えずに熱から仕事は取り出せません。これがトムソンの原理です。等温膨張と混同してはいけませんよ。
■クラウジウスの原理
物理学の教科書では次のように書いてあります。
低温の熱源から高温の熱源に正の熱を移す以外に、 他に何の痕跡も残さないようにすることは出来ない。
同じように解釈すると、他に何も変化を残さずに、低温物体から高温物体へ熱を移すことは不可能であるという意味になります。クラウジウスの原理は経験的にわかりやすいかもしれません。低温熱源と高温熱源を置いておくと何もしなくても(何の状態も変えなくても)高温熱源に低温熱源から熱が移動できてしてしまう。しかし、そんなことは起こり得ないことなど皆さんもご存じでしょう。
■クラウジウスの原理とトムソンの原理の同等性
クラウジウスの原理とトムソンの原理は、実は全く同じなのです。クラウジウスの原理がなりたてば、トムソンの原理がなりたつし、トムソンの原理が成り立てばクラウジウスの原理もなりたちます。子の証明については、下記のサイトの説明にゆだねます。確認のほどよろしくお願いします。
参考1)http://homepage3.nifty.com/rikei-index01/neturiki/neturiki2nado.html
参考2)http://camellia.thyme.jp/files/html/thermo20130322/node56.html
■オストワルドの原理
これは非常にシンプルな原理です。第2種永久機関は存在しない。第二種永久機関とは、「一つの熱源から正の熱を受け取り、これを全て仕事に変える以外に、 他に何の痕跡も残さないような機関」のことです。必然的にトムソンの原理が成り立てばオストワルドの原理もなりたつのです。第二種という表現から第一種はなんだという疑問が生じますよね。永久機関は昔の人のロマンでした。
第一種永久機関=無からエネルギーを生み出す熱機関
第二種永久機関=元の状態に戻りながら熱エネルギーを100%仕事にする熱機関
として、研究されてきたのですが第二種永久機関は存在しないのです。
忍者カウンター
カレンダー
カテゴリー
フリーエリア
最新記事
(04/05)
(01/18)
(01/18)
(01/18)
(01/18)
プロフィール
HN:
こうちゃん。
性別:
非公開
ブログ内検索
最古記事
(01/24)
(09/07)
(09/07)
(09/12)
(09/12)

