2成分系状態図‐ベンゼン‐トルエン

ベンゼンのモル分率をx1,蒸気圧をP1とする。
トルエンのモル分率をx2,蒸気圧をP2とする。

ここで、モル分率の定義より2成分系では次式が成り立つ。

x1+x2 = 1 …①

さらに、全蒸気圧をPとしてドルトンの分圧の法則より、分圧について次式が成り立つ。

P = P1+P2…②

ここで、理想溶液ではラウールの法則が成り立つので、任意の成分iに対して次式が成り立つ。

Pi = pi＊xi　…③

piは純物質における蒸気圧である。この式を用いて②式を変形すると、

P = p1*x1+p2*x2 = p1*x1+p2*(1-x1) = (p1-p2)*x1 + p2 …④

あるいは、

P = p1*x1+p2*x2 = p1*(1-x2)+p2*x2 = (p2-p1)*x2 + p1…⑤

と変形できる。ここで、ベンゼンとトルエンの純物質時の蒸気圧は20℃でそれぞれ
75.0、27.0　Torrであり、代入すると下記の式のようになる。

P=48x1＋27.0　…④’　
P＝75－48x2　 …⑤’

ベンゼンのモル分率x1に対して、P,P1,P2をプロットしたのが下の図である。


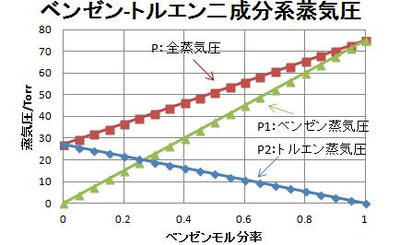
最後に蒸気になった分子のモル数を求めておこう。

ベンゼン、トルエンの蒸気中のモル数をy1,y2とするとドルトンの分圧の法則より

y1 = P1/P = p1x1/{ (p1-p2)*x1 + p2 } = 75x1/(48x1+27.0)…⑥
y2 = P2/P = p2x2/{(p2-p1)*x2 + p1} = 27x2/(75-48x2)…⑦

以上より、液相中のベンゼンモル分率x1と蒸気圧P,蒸気中のベンゼンモル分率y1とPをプロットしたグラフが下の図である。前者を液相線、後者を気相線という。




以上が状態図の入門である。