■カルノーの定理の証明前回、
カルノーサイクルの概要と効率の計算の仕方を論じました。
今回はもう少し議論を発展させて、カルノーの定理について論じます。カルノーの定理の前に一つ論じておくことがあります。それは、カルノーサイクルが可逆か不可逆かです。カルノーサイクルは、結論からいうと可逆機関です。そもそも、カルノーサイクル自体が可逆過程を組み合わせたものであり、逆に回すことも可能なのです。そこを踏まえたうえでカルノーの定理を考えてみましょう。カルノーの定理とは、下記の定理です。
■定まった高温熱源と低温熱源の間に働く熱機関サイクルのうち、全ての可逆サイクルは等しく最大であり、不可逆サイクルは必ずそれより小さい。何の話をしているかというと、こういうことです。｢高温熱源と低温熱源がある熱機関だとカルノーサイクル(可逆サイクル)は全部同じ効率であり、カルノーサイクルが最大効率を持ったサイクルです。よって、不可逆サイクルはそれより効率が低くなります｣といっているのです。
よく、オットーサイクルやランキンサイクル等の実サイクルも可逆サイクルだから、カルノーの定理よりカルノーサイクルと同じ効率では？と思われる方がいる。そもそも前提である熱源の個数がずれています。カルノーの定理は【ただ２つの熱源の間で動作する可逆機関】を対象として議論をしています。でも、実サイクルはそうではありません。例えば、実サイクルの可逆機関では等圧変化過程や等積変化過程があります。これらの過程では必ず熱の出入りがあります。準静的変化(可逆変化)では，熱の移動の時に温度差があってはいけませんから例えば等圧変化で温度が Ta から Tb まで変化したとすると，熱をやりとりする相手の熱源は温度が Ta から Tb までの連続無限個のものが必要になります．
したがって，カルノーサイクル以外のものは【ただ２つの熱源の間で動作する可逆機関】ではないのです。ここは誤解しないでください。同じディスカッションがYahoo知恵袋にありますので紹介しておきます。
http://okwave.jp/qa/q5374013.html
じゃあ、何故カルノーの定理が成り立つのか。今回はこれについて解説しようと思います。
すべての可逆サイクル(カルノーサイクル)の効率は等しい。(証明)可逆サイクルAと可逆サイクルBの効率をηAとηBを定義する。今、ηA＞ηBだと仮定しサイクルAとサイクルBを連結したサイクルを考える。(下図参考)
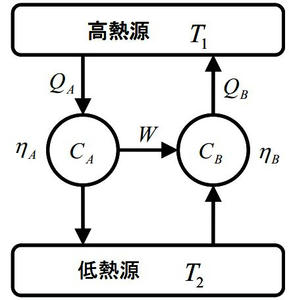
上のサイクルではηA>ηBより、W/QA > W/QB ⇔QB > QAとなるが、この場合低温熱源から高温熱源に移動することになり、熱力学の第二法則に反する。よってηA≦Bでなければならない。
※そもそも可逆サイクル同士の組み合わせですから、このケースの場合、何の影響も残さずに低温熱源から高温熱源に熱を移動させていますよね。
じゃあ、ηA＜ηBとなる場合はどうかというと、下記の図を見てください。
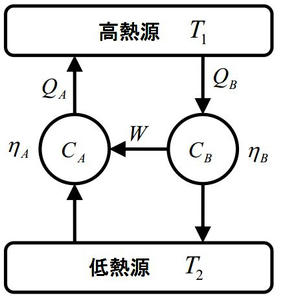
図のように可逆サイクルを回すとηA＜ηB⇔W/QA<W/QB⇔QB<QAとなり、低温熱源から高温熱源に何の影響も残さず可逆的に熱の移動ができてしまう。これもまた矛盾だといえます。
二つの熱源の場合、可逆機関の熱効率はηA＝ηBとなり等しくならざるをえないのです。
不可逆サイクルの効率は必ず可逆サイクル(カルノーサイクル)に劣る。これを証明するために、可逆サイクルと不可逆サイクルを組み合わせた図のようなサイクルを考えましょう。
不可逆サイクルの効率をη’、可逆サイクルの効率をηとする。
η’＞ηと仮定すると、W/Q'>W/Q⇔Q>Q'となり、やはり熱力学第二法則に矛盾する。よってη’≦ηとなる。更にη’＝ηとするとQ'=Qとなるが、これでは不可逆サイクルと可逆サイクルの連結サイクルが可逆サイクルになってしまうので矛盾しています。以上より、η’＜ηとならざるをえないのです。
これにより二つの熱源からなる可逆サイクル(カルノーサイクル)こそが、最大の熱効率を誇る熱機関だということが証明されました。更に、カルノー効率は前回の記事によると
η = 1- TL/TH = (TH - TL)/TH ＜ 1です。
従って、η＝1となる熱機関は作ることができないのです。第二種永久機関は存在しない。カルノーの功績から定量的に理解できると思います。それにもかかわらず、カルノー自身は熱力学第二法則の発見者ではないのですよね。それでも、物理学が進んだ現代だからカルノーの功績の素晴らしさは理解できるものだと思いますよ。
追記：実はこれまで理想気体でカルノー効率を定義したので、腑に落ちないかもしれませんがやはり実在気体であっても上のような効率になります。やはりすべてのカルノーサイクルは同等なのです。これを導出するヒントは、http://qanda.rakuten.ne.jp/qa1885802.htmlに論じられていますが、暇な時やっておきます。
■クラウジウスの不等式
さて、ここまで二つの熱源に対して下記が成り立つことを論じました。
QH/TH + QL/TL = 0 …①
不可逆過程の場合は、上の＝が成り立ちません。カルノーの定理より
η = W/QH = (QH＋QL)/QH < (TH - TL)/TH
⇔1 ＋ QL/QH < 1 - TL/TH
⇔QL/QH + TL/TH < 0
⇔QL/TL + TH/QH <0…②
となります。従って一般の機関に対して下記が成り立つのは自明です。
QH/TH + QL/TL ≦ 0 …③
さて、2個の熱源で上の式が成り立つことがわかりました。
これをN個の熱源に拡張した議論がクラウジウスの不等式です。
クラウジウスの不等式では複数個の熱源に対して下記が成り立つという議論です。
ΣQi/Ti ≦0(∞個の熱源に拡張すると∮dQ/T≦0)
では、何故この式が成り立つのか？次回の記事ではそれについて論じようと思います。
[12回]
PR
COMMENT